
線対称と点対称の違いを十分理解して混同しないこと
算数では線対称と点対称についても勉強をします。しっかりと考え方を理解していない子供ですと正解までたどり着けなくなってしまいますので、違いに注意をしながら学習していきましょう。
まず、線対称ですがある図形を線をもとに対称となる移動を行うということです。元の図形上にあるすべての点は移動後は軸となった直線と90度で交わる直線上で等距離の場所に移動することになります。
一方で、点対称とはある点を中心に180度回転したところに移動するということです。回転移動がベースになっているということになります。もとの図形上にあるすべての点は回転の中心点との直線上で等距離の場所に移動することになります。
これだけですと、少々分かりずらいと思いますので、下の図を見ながら考えていくことにしましょう。
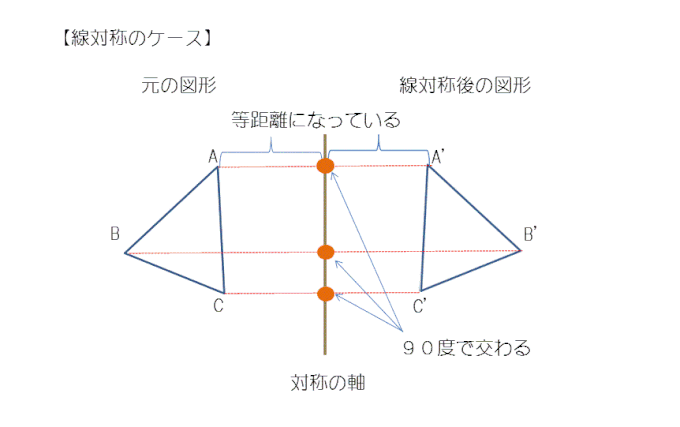
まずは、線対称のケースですが、元の図形である三角形のA,B,Cがそれぞれ対象の軸で線対称した後の図形である三角形のA',B',C'に移動しています。
そのとき、対象の軸からAまでの距離と対象の軸からA'までの距離は等しくてさらに90度で交わるということになります。
次に点対称のケースですが、元の図形である三角形のA,B,Cがそれぞれ点Oを中心として点対称した後の図形である三角形のA',B',C'に移動しています。
このとき、点Oを中心として180度回転しているのですから、Aから中心Oまでの距離とA'から中心
Oまでの距離は等しくなるということになります。

図形問題が得意な子供は沢山のことを頭の中で想像することが出来る子が多いです
図形問題は基本的な事が理解できたのであれば、いろいろなケースを多面的に考えてみることが上達の秘訣です。しっかりと線対称と点対称の基本を学んでから様々なケースを想像しながら勉強を進めることでグングンと実力が伸びていくことでしょう。
特に、線対称や点対称の問題は基本的な事が理解できたらいくつかの応用問題を考えてみると算数の楽しさを子供が実感できるようになってくると思います。
少し応用パターンを紹介しますので、いろいろと想像力を膨らましてみてください。
【線対称を2回おこなうケース】
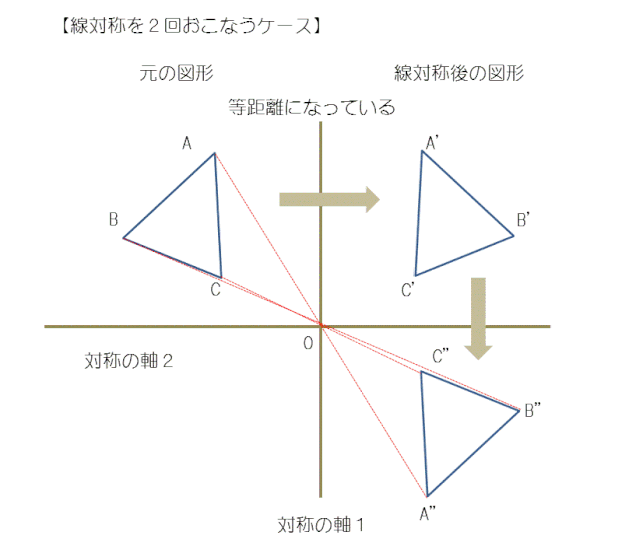
元の図形を対称軸1に対して右側に線対称を行い、続いてさらに90度で交わる対称軸2に対して下に線対称を行うと三角形A"B"C"に移動します。
これは、よく見ると元の三角形を2つの対象の軸の交点Oを中心として点対称したことと同じ結果になります。
続いて、点対称ですが、回転の中心Oが元の図形の内側にあると点対称後の図形がイメージしにくくなってしまいますので気を付けましょう。
【点対称で回転の中心が元の図形の内側にあるケース】
考え方は通常の点対称と全く同じですが、回転後にどのような位置に動いたかをしっかりと理解できるようにしましょう。

他にもさまざまなケースがありますので、楽しみながら勉強を進めていきましょう。






