台形の面積の公式は柔軟な思考で覚えるようにすること

小学校の算数で学ぶ四角形の一つに台形があります。まずは、台形の定義をしっかりと理解することから始めましょう。大人の方でも台形の定義となると説明できないかもしれませんが、しっかりと台形の特徴を理解していれば、なるほどと感じることでしょう。

台形とは、１組の対辺が平行で、もう１組の対辺は平行ではない四角形をいいます。２組の対辺が平行であれば、平行四辺形になりますが、台形の場合は１組だけが平行というところがポイントになります。しっかりと各四角形の特徴をおさえてしっかりと定義が説明できるようになるのが図形を得意にするうえで重要です。

さて、台形の特徴をしっかりと学んだのであれば、次に大切な事といえば、面積の公式です。もちろん公式がありますので、それを覚えてしまえばいいわけなのですが、どうしてそのような公式になるのかという柔軟な思考で考えるようにしてみましょう。

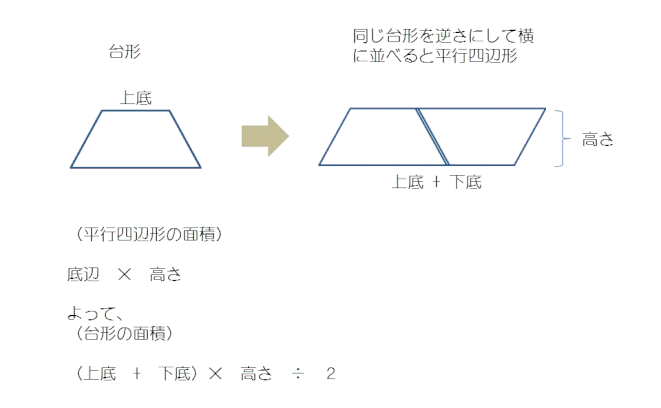
台形の面積を求めるには同じ形の台形２個を想像してみると分かりやすいです

上の図のように、元の台形をもう１つ作って、上下さかさまにして２つを並べてみることで台形の面積の求め方のイメージが湧くと思います。このように台形を２つ横並びに並べると、今度は平行四辺形になっているのが分かると思います。

ですので、台形の面積は平行四辺形の面積の公式と深い関係があるということになります。平行四辺形の面積は底辺×高さということになりますので、この図の台形２つ分の面積は（上底+下底）×高さ

です。ただし、これは同じ台形２つ分の面積となっていますので最後に２で割るということになるのです。

台形の面積の求め方には公式がありますので、小学生の子供が暗記をしてそのまま使うことも可能です。しかし、どうしてこのような式になるのかということを本当に理解しているのかどうかはとても重要な事です。正しく理解ができているのであれば、公式を知らなくても面積を求めることが出来るはずです。

算数の中でも図形の分野は柔軟な思考力が必要です。様々な視点で図形を見る力がなければ応用問題を解くことが出来ません。できるだけ暗記に頼ることなく、柔軟な思考力を培っていくように考える楽しみを知ってもらうということを心がけましょう。